Winkelfunktionen-Rechner
Sei es im Bereich der Mathematik, im beruflichen, technischen oder privaten, immer wieder mal begegnet uns das wir eine Winkelfunktion berechnen müssen. In den technischen Berufen, vor allem Architekten, ist die Winkelberechnung unumgänglich. Genauso auch im handwerklichen Beruf, hier müssen auch immer wieder Berechnungen durchgeführt werden. Winkelfunktionen zeigen geometrische Winkel und Längenverhältnisse, diese können einfach berechnet werden und werden auch als Trigonometrie bezeichnet.
Stell uns deine Frage. Wir antworten dir schnellstens...
Wie rechnet der Winkelfunktionen-Rechner?
Zur Berechnung eines beliebigen Dreieckes müssen drei Werte gegeben sein, davon mindestens eine Seitenlänge. Die Winkel müssen im Gradmaß angegeben werden.
Die Nachkommastellen können von 0 – 15 ausgewählt werden, je mehr Nachkommastellen, desto genauer das Ergebnis.
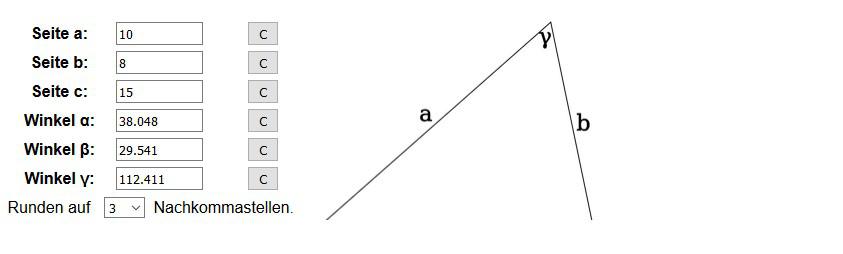
Das Ergebnis
Bei der Berechnung werden die restlichen Werte oben neben dem Dreieck automatisch mit eingefügt und im unten Feld wird dann die weitere Berechnung durchgeführt. Wir haben in unserem Beispiel die Seiten a, b und c angegeben und 3 Nachkommstellen ausgewählt. Die Winkel ? (Alpha), ? (Beta) und ? (Gamma) wurden somit ergänzt.
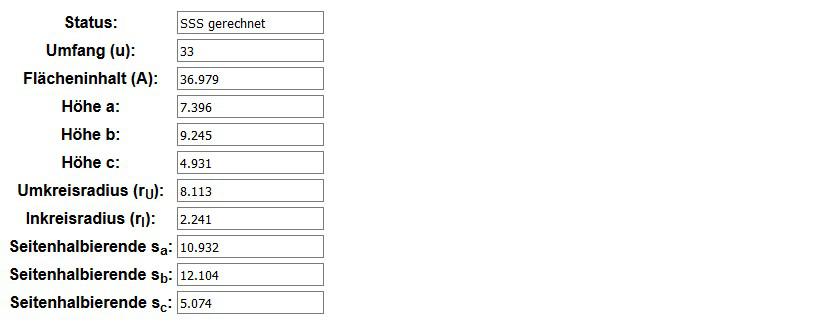
Das Ergebnis ermittelt Umfang, Flächeninhalt, Höhe der Seiten a, b und c, Umkreisradius, Inkreisradius und die Seitenhalbierende Sa, Sb und Sc.
Die Seitenhalbierende wird auch Schwerlinie oder Median genannt und ist die Strecke, die eine Ecke mit dem Mittelpunkt der Seite verbindet, die gegenüberliegend ist.
Für eine übersichtlichere Darstellung der Berechnung hier einmal das Ergebnis mit geraden Zahlen ohne Nachkommastellen.
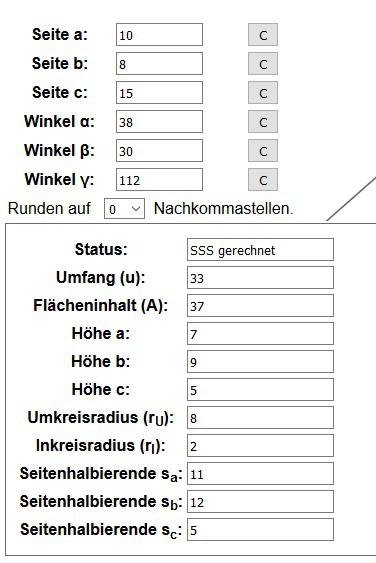
Das Dreieck
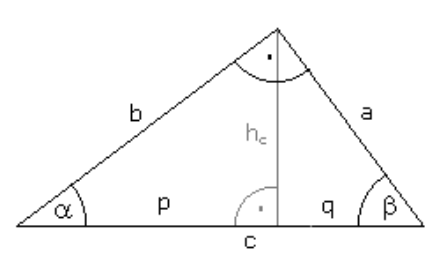
Wie die meisten mathematischen Körper hat auch das Dreieck seine Bezeichnungen und Formeln zur Berechnung.
Auch bei der Winkelfunktionsrechnung ist eine Kombination aus Buchstaben und griechischen Buchstaben zu finden sowie lateinische Namen, wie wir es öfter in der Mathematik finden.
Umfang (u) = Seite a + Seite b + Seite c
Flächeninhalt (A) = a x b / 2
Kathetensatz = Seite a2 = c x p
Hypotenuse = p + q = c
Satz des Pythagoras = a2 + b2 = c2
Winkelsumme = ? + ? = 90°
Trigonometrie:
Sin (?) = Gegenkathete / Hypotenuse oder auch a / c
Cos (?) = Ankathete / Hypotenuse oder auch a / b
Tan (?) = Gegenkathete / Ankathete oder auch a / b
Bezeichnung der einzelnen Kürzel und Grundlagen zum Dreieck:
Die Ecken werden mit den Großbuchstaben A, B und C gekennzeichnet und zwar gegen den Uhrzeigersinn. Die Seiten werden mit den Kleinbuchstaben a, b und c bezeichnet, wobei jeweils die Seiten immer gegenüber dem gleichnamigen Eckpunkt liege, a zu A, b zu B und c zu C.
Die Winkel werden mit ? (Alpha), ? (Beta) und ? (Gamma) benannt und sind an den jeweiligen Eckpunkten A, B und C. Der rechte Winkel hat immer 90°, derjenige der größer als 90° ist, ist der stumpfe Winkel und der kleiner als 90° ist, ist der spitze Winkel.
Die Hypotenuse ist die längste Seite bei einem rechtwinkligen Dreieck und liegt immer gegenüber dem rechten Winkel.
Die beiden kürzeren Seiten nennt man Katheten, sie bilden den rechten Winkel. Zur Unterscheidung werden sie als Ankathete und Gegenkathete bezeichnet. Die Benennung der Katheten hängt davon ab, auf welchen Winkel man sich bezieht. Die Ankathete ist die dem anliegenden Winkel Kathete, die Gegenkathete ist diejenige, die dem Winkel gegenüberliegt.
Ein paar Grundlagen zum einfachen Merken:
Die Seite a wird als Gegenkathete bezeichnet, sie liegt gegenüber ? (Alpha). Seite b ist die Ankathete, sie liegt im Winkel von ? und Seite c wird als Hypotenuse bezeichnet.
Bei einem rechtwinkligen Dreieck finden wir Sinus, Cosinus und Tangens. Der Sinus (sin) eines Winkels ist das Verhältnis der Gegenkathete (zur Kathete, die dem Winkel gegenüber liegt) zur Hypotenuse, also der Seite gegenüber dem rechten Winkel. Der Cosinus, auch Kosinus (cos) ist das Verhältnis der Ankathete zur Hypotenuse. Und der Tangens (tan) eines Winkels ist das Längenverhältnis von der Gegenkathete zur Ankathete.
Der Seite mit dem rechten Winkel, dem 90° Winkel, liegt die Hypotenuse immer gegenüber und ist auch die längste Seite des Dreieck.
Die Seite, die direkt dem Winkel ? anliegt ist somit die Ankathete und die gegenüberliegende Seite heisst dann Gegenkathete.
Die Winkelberechnung ist somit eine wertvolle Berechnungsmethode und mit unserem Rechner um ein vielfaches leichter und einfacher. Das Ergebnis ist schnell ermittelt und es werden einige mehr Details ausgegeben, die sehr hilfreich sein können, je nachdem für welchen Zweck die Berechnung durchgeführt wird.

