Polynomdivision-Rechner
Die Polynomdivision ist ein Rechenverfahren in der Mathematik zur Division von Zahlen mit Rest. Nur werden hier anstelle von zwei Zahlen zwei Polynome durch einander dividieren im Ergebnis wieder zu Polynome – zu Ganzteil und Rest der Division.
Polynomdivision-Rechner
Stell uns deine Frage. Wir antworten dir schnellstens...
Das Wort Polynom kommt aus dem griechischen: poly = viel und Nomos = Satzung, Gesetz. Ein Polynom ist eine (endliche) Summe von Vielfachen von Potenzen mit natürlichzahlingen Exponaten einer Variablen, die unendliche Summe wird als Potenzreihen benannt. Oder einfach gesagt, die Polynomdivision berechnet Nullstellen von Polynomen.
Die Art und Weise der Berechnung ähnelt der schriftlichen Division, wie man es schon in der Grundschule lernt. Die Variable wird meistens mit x bezeichnet.
Wie funktioniert der Polynomdivision Rechner
In das Formular wird eigentlich nur die Berechnung bzw. die Rechenaufgabe, deren Ergebnis berechnet werden soll eingetragen.
In das rechte Feld kommt der Dividend, in das linke Feld der Divisor.
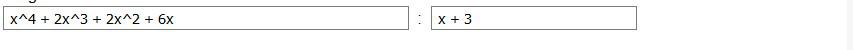
Das Ergebnis
Das Ergebnis zeigt nun aufgeschlüsselt wie man das Ergebnis berechnen kann mit dem genauen Rechenweg. Wie man erkennen kann ist auch hier mit der schriftlichen Division das Ergebnis ermittelt.
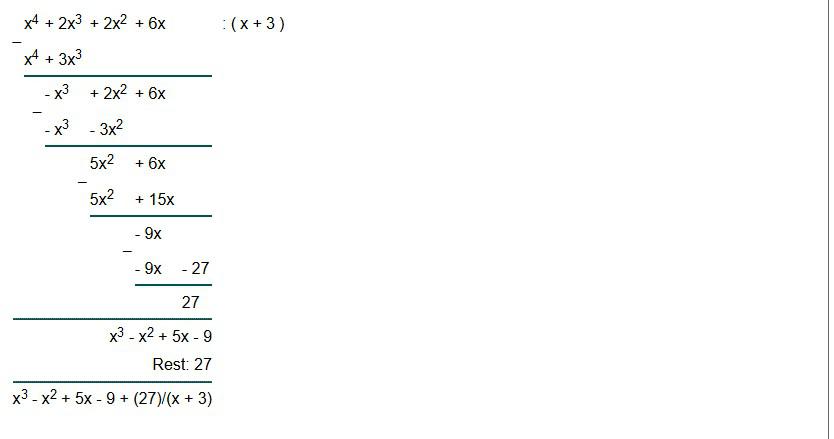
Erklärung des Ergebnisses
Genauso wie bei der schriftlichen Division werden auch bei der Polynomdivision vom Dividenden nach und nach passende Vielfache des Divisors abgezogen, sodass man Ende nach Möglichkeit kein Ret mehr bleibt.
In jedem Schritt wird derjenige Summand des Restes eliminiert, der x in der höchsten Potenz stehen hat. Die Summanden des Quotienten erhält man nun durch Division dieser Summanden der jeweiligen Reste und durch den Summanden des Divisors, der die höchst Potenz von x hat.
x^4 + 2x^3 + 2x^2 + 6x
Der Summanden des Restes der die höchste Potenz hat ist x^4.
Weil x^4/x = x^3 ist, ist der erste Summand des Quotienten x^3.
x^3 wird folgendermaßen berechnet: x^3·(x + 3) = x^4 + 3x^3, dies vom Rest subtrahieren, der neuer Rest ist -x^3 + 2x^2 + 6x.
Nun ist der Summand des Restes der die höchste Potenz von x hat x^3.
Dann wird der nächste Rechenschritt ausgeführt:
Weil x^3/x = -x^2 ist, ist der erste Summand des Quotienten x^2.
x^2 wird folgendermaßen berechnet: x^2·(x + 3) = -x^3 – 3x^2, dies vom Rest subtrahieren, der neuer Rest ist -5x^2 + 6x.
Nun ist der Summand des Restes der die höchste Potenz von x hat 5x^2.
Und der nächste Rechenschritt:
Weil 5x^2/x = 5x ist, ist der erste Summand des Quotienten x^5.
x^5 wird folgendermaßen berechnet: 5x·(x + 3) = 5x^2 + 15x, dies vom Rest subtrahieren, der neuer Rest ist -9x.
Nun ist der Summand des Restes der die höchste Potenz von x hat -9x.
Und ein letzter Rechenschritt:
Weil -9x/x = -9 ist, ist der erste Summand des Quotienten -9.
-9 wird folgendermaßen berechnet: -9·(x + 3) = -9x – 27, dies vom Rest subtrahieren, der neuer Rest ist 27.
Der Rest hat einen kleineren Polynomgrad (g=0) als der Divisor (g=1), daraus resultiert Abbruch. Nun wird der Quotient durch den Summanden „Rest/Divisor“ ergänzt.
Somit ergibt sich das Ergebnis der Polynomdivision: x^3 – x^2 + 5x – 9 + 27/(x + 3)
Wie funktioniert die Polynomdivision
Bei diesem Verfahren werden nicht nur zwei Zahlen dividiert, sondern ganze Terme. Term bezeichnet einen sinnvollen Ausdruck, dieser kann Zahlen, Variablen, sowie Symbolen, die für die mathematischen Verknüpfungen verwendet werden, und Klammern enthalten.
Zur Berechnung braucht man einen Term und eine Nullstelle dieses Terms. Hierbei handelt es um Polynome. Ein Polynom wird durch ein Polynom geteilt, das ist die Polynomdivision.
Es ist nicht immer so einfach die Nullstelle zu finden, wenn sie nicht vorgegeben ist kann sie durch das numerische Verfahren oder einfach durch Raten gefunden werden.
Die Polynomfunktion ist in der elementaren Algebra eine Funktion P der Form:
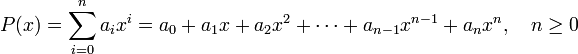
Quelle Wikipedia
Anwendungen für eine Polynomdivision
Die Division kann bei verschiedenen Gleichungen und Verfahren angewendet werden.
Bei Kurvendiskussionen zur Bestimmung der Näherungskurven von einer rationalen Funktion.
Zum Lösen von Gleichungen höchsten Grades. Wenn eine Lösung xn beispielsweise durch Intervallschachtelung gefunden wird, so findet die Polynomdivision Anwendung, damit der Grad der Gleichung um Eins gesenkt wird.
Zur Berechnung von Prüfsummen.
Zur Partialbruchzerlegung von rationalen Funktionen.
Ist eine Polynomdivision erfolgt, so kann dasselbe Verfahren auch auf Divisor und Rest erneut angewendet werden, so kann ein weiterer Rest berechnet werden usw. Dann erhält man die sogenannte Polynomrestfolge.

