Matrizenrechner – Matrix berechnen
Man rechnet mit Matrix A und Matrix B und in der Ergebnismatrix wird wie der Name sagt das Ergebnis ausgegeben
Matrizenrechner
Stell uns deine Frage. Wir antworten dir schnellstens...
Der Begriff Matrizen, im Singular Matrix ist ein Begriff aus der Mathematik bzw. aus der linearen Algebra. Das sind rechteckige Anordnungen / Tabellen von mathematischen Elementen, wie Variablen oder Zahlen, mit denen im Ganzen gerechnet werden kann. Sie werden überwiegend zur Darstellung von linearen Abbildungen verwendet und beschreiben lineare Gleichungen. Gerechnet wird mit Matrizen indem sie addiert oder multipliziert werden.
Die Bezeichnung wurde 1950 eingeführt von James Joseph Sylvester (1814 – 1897).
Man rechnet mit Matrix A und Matrix B und in der Ergebnismatrix wird wie der Name sagt das Ergebnis ausgegeben. Matrizen können addiert oder multipliziert werden und können beliebige Dimensionalität besitzen. Auch die Dimensionalität ist ein Begriff aus der Mathematik und bezeichnet ein Konzept, welches im Wesentlichen die Anzahl von Freiheitsgrade einer Position und/oder Bewegung in einem bestimmten Raum bezeichnet.
Der Freiheitsgrad (F bzw. f) bezeichnet bei kinematischen Ketten, auch Laufgrad, die Zahl der voneinander unabhängigen Bewegungsmöglichkeiten, diese sind die diesem Sinn „frei wählbar“. Die Bewegungsmöglichkeiten werden auch Freiheiten genannt. Ein starrer Körper hat den Freiheitsgrad 6 und zwar deshalb, weil er in drei voneinander unabhängigen Richtungen bewegt und um drei voneinander unabhängigen Achsen gedreht werden kann.
Wie funktioniert der Matrizenrechner?
In den Matrizenrechner können nun in 2 Tabellen die Zahlen eingetragen werden, wobei es mehrere Optionen und Varianten gibt.
Bei Matrix A und B kann jeweils der Rang von 1 bis 10 ausgewählt werden.
In die Tabelle können bis zu 9 Zahlen eingetragen werden, oder auch gefüllt bzw. aufgefüllt werden mit Mullmatrix, Einheitsmatrix und Ergebnismatrix.
Bei der Operation gibt es dann wieder mehrere Möglichkeiten zur Auswahl, das sind:
A + B, A – B, B – A, A * B, B * A, Transponiere A, Transponiere B.
Die Auswahlmöglichkeiten sind jeweils über ein PullDown Menue zu wählen
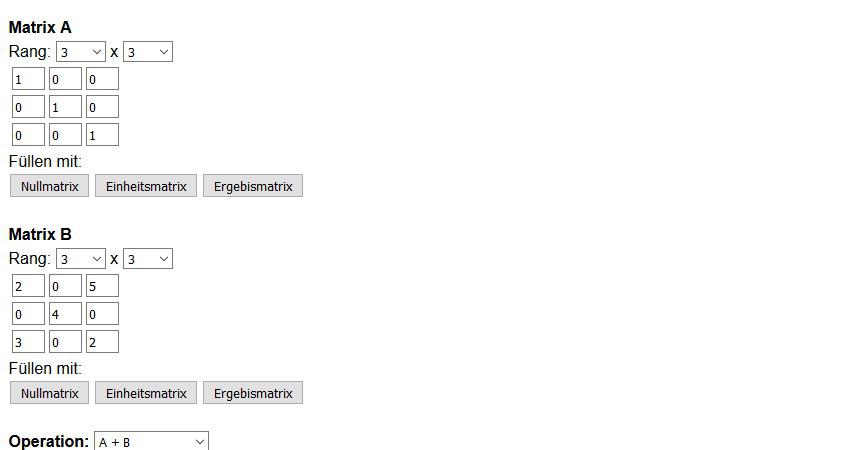
Das Ergebnis

Das Ergebnis zeigt nur Matrix A + Matrix B. Es ist leicht zu erkennen wie Matrizen berechnet werden.
Die Berechnung kann der Matrix kann bis zu 10 x 10 erweitert werden.
Zur Auswahl zum berechnen steht auch u.a. Transponiere A, Transponiere B. Doch was ist transponieren? Die transponierte Matrix, auch gespiegelte Matrix oder gestürzte Matrix genannt, entsteht durch vertauschen von Zeilen und Spalten. Dabei entspricht die erste Zeile dieser Matrix der ersten Spalte der Ausgangsmatrix, zweite Zeile zweite Spalte usw. Veranschaulicht kann man sich die transponierte Matrix durch eine Spiegelung von der Ausgangsmatrix an ihrer Hauptdiagonale vorstellen.
Zur Berechnung von Hand sind einige umfangreiche Formeln nötig, die entsprechend erweitert und verändert werden können, so kann das Ganze schon kompliziert und umfangreich werden. Da ist der Matrizenrechner eine sehr große Erleichterung.

