Determinanten Rechner
Die Determinante, Mehrzahl Determinanten, ist eine spezielle Funktion in der linearen Algebra. Sie wird einer quadratischen Matrix (auch Quadratmatrix, n Zeilen und n Spalten) bzw. allgemein einem Endomorphismus einen Skalar (mathematische Größe) zugeordnet.
Determinanten Rechner
Stell uns deine Frage. Wir antworten dir schnellstens...
Mit Determinanten kann beispielsweise festgestellt werden, ob ein lineares Gleichungssystem eindeutig lösbar ist, sowie zur Flächenberechnung und dem Invertieren von Matrizen.
Die Lösung kann mit Hilfe der Cramersche Regel, auch Determinanten Methode genannt, dann explizit angegeben werden. Das Gleichungssystem ist dann eindeutig lösbar, wenn Determinante und Koeffizientenmatrix ungleich null ist. Eine quadratische Matrix ist genau dann invertierbar, wenn ihre Determinante dann ungleich null ist.
Die Cramersche Regel ist benannt nach Gabriel Cramer, die im Jahr 1750 veröffentlicht wurde, jedoch schon vorher von Leibniz gefunden wurde.
Für Determinanten (abgekürzt in der Formel mit det, A oder detA) gibt es verschiedene Schreibweisen. Als Funktion, wobei dann die Matrix der Parameter der Funktion ist. Und als senkrechte Striche, die sogenannten Betragsstriche, womit eine Variable, die eine Matrix definiert, bzw. eine Matrix selber geschrieben wird. Ja nach Schreibweise wird dann abgekürzt mit |A| oder det(A).
Beispiel: die 2 x 2 Matrix
![]()
die Determinante
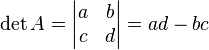
Wie funktioniert der Determinanten Rechner?
Die Tabelle als Grundlage für die Berechnung erinnert an den Matrizen Rechner und auch hier wird somit die Matrix eingetragen. Der Rang kann von 1 bis 10 berechnet werden, so hat das Quadrat beispielsweise bei Rang 3 eine Größe von 3 x 3 = 9 und bei Rang 10 eine Größe von 10 x 10 = 100.

Das Ergebnis

Zur Verdeutlichung hier einmal eine 3×3 Matrix aufgeschlüsselt in ihre Berechnungsgrundlage.
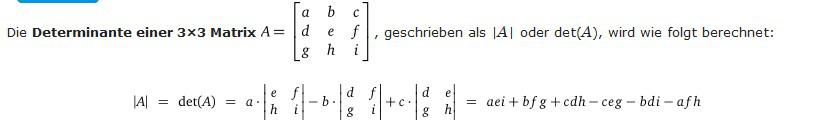
Ein paar Grundregeln zur Berechnung
Man berechnet Determinanten bis n=4 im Dezimalmodus, danach als Dreieckmatrix nach Gauß-Verfahren, wobei dann unterhalb der Diagonale nur noch Nullen stehen. Die Berechnung erfolgt Zeilenweise durch Überprüfung nach der Zahl 0. Steht in der Zeile kein 0 wird eine Spalte weiter gesucht. Ist eine 0 zu finden, so wird diese Zeile addiert, sonst bricht der Algorithmus ab, denn die Zeilenvektoren sind dann nicht linear unabhängig damit die Determinante sicher 0 beträgt.
Indem dann zu allen weiteren Zeilen unterhalb der letzten Zeile mit 0 die passende Vielfache addiert werden, können dann die Elemente zu 0 gemacht werde. Die Vielfache ändert durch addieren den Wert der Determinanten nicht, da der Rechner dieses berücksichtigt.
Das Gauß-Verfahren benannt nach Carl Friedrich Gauß (1777 bis 1855) ist ein Algorithmus der linearen Algebra und ist ein Verfahren eben von linearen Gleichungen und beruht auf elementare Umformungen von Gleichungssystemen um eine Lösung zu erhalten.
Ursprünglich definierte man Determinanten als eine Eigenschaft linearer Gleichungssysteme. Sie determiniert (daher die Ableitung zum Begriff) ob diese Gleichung eine eindeutige Lösung hat. Das ist der Fall, wenn die Determinante ungleich 0 ist. Hieraus resultieren die 2×2 Matrizen nach Gerolamo Cardano (1501 bis 1576) Ende des 16. Jahrhundert und etwa 100 Jahre später größere Matrizen nach Gottfried Wilhelm Leibniz (1646 bis 1716).
Jeder quadratischen Matrix kann eine eindeutige Zahl zugeordnet werden, die dann als Determinante der Matrix bezeichnet wird. Diese wird durch eine Formel definiert wobei die Summe über alle Permutationen ? zu erstrecken ist.
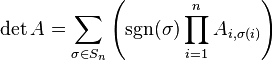
Bei einer 2 x 2 – Matrix wird die Determinante nach dieser Formel berechnet:
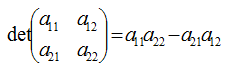
Eine 3×3 Determinante kann nach der Sarrusschen-Regel, auch Jägerzaun-Regel berechnet werden. Hierbei werden die Elemente der Hauptdiagonalen multipliziert und die Werte addiert, davon dann die Werte der Nebendiagonalen subtrahiert. Sie ist benannt nach dem französischen Mathematiker Pierre Frédéric Sarrus (1798 bis 1861).
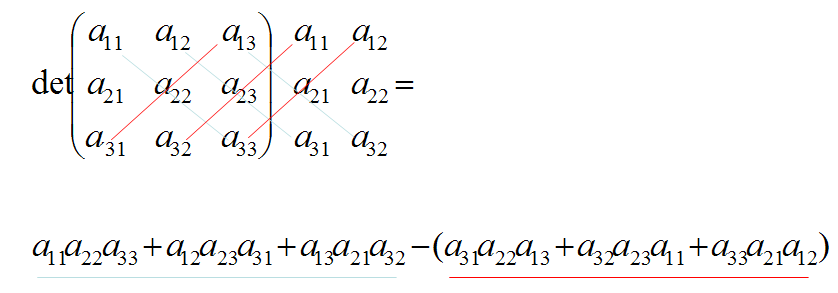
Sind die Determinanten größer, so werden sie nach dem Laplaceschen Entwicklungssatz auf kleinere Determinanten zurückgeführt, also kleiner berechnet. Sie werden nach einer beliebigen Spalte oder Zeile entwickelt wobei das Vorzeichen alterniert.
Sie können auch nach dem Gauß-Verfahren berechnet werden, wobei hier die Determinante durch eine Umformung in beispielsweise Dreiecksform gebracht wird.
Letztendlich ist die Berechnung von Determinanten ziemlich komplex und der Rechner erleichtert einiges und ist dazu noch besonders schnell und genau.
