Quadratische Ergänzung Rechner
Die quadratische Ergänzung ist ein Verfahren in der Mathematik bzw. Algebra, dass zum Umformen von Termen, bei denen eine Variable quadratisch vorkommt. Der Term wird dabei so umgeformt, dass entweder die erste oder die zweite binomische Formel angewendet wird. Das Ziel ist, dass am Ende ein quadriertes Binom als Ergebnis herauskommt bzw. entsteht.
Stell uns deine Frage. Wir antworten dir schnellstens...
Der Grund, warum ein Term so umgeformt wird, dass ein quadriertes Binom entsteht liegt drin, dass mit Hilfe der quadratischen Ergänzung eine quadratische Funktion in Scheitelpunkt gebracht werden kann und auch quadratische Gleichungen gelöst werden können.
Der Scheitelpunkt, auch Scheitelform genannt, ist eine bestimmte Form einer quadratischen Gleichung, aus der eben der Scheitelpunkt abgelesen werden kann. Dieser ist entweder der höchste oder tiefste Punkt einer Parabel. Bei einer nach oben geöffneten Parabel ist der Scheitelpunkt der tiefste Punkt, auch Minimum der Funktion, bei einer nach unten geöffneten Parabel ist dieser der höchste Punkt, auch Maximum der Funktion.
Die allgemeine Form einer quadratischen Funktion:
f(x)=ax2+bx+c
Die Scheitelpunktform einer quadratischen Funktion
f(x)=a(x?d)2+e
Wie funktioniert der quadratische Ergänzung Rechner?
Die Gleichung wird einfach in das Formular ergänzt. Wobei plus (+) oder minus (–) ausgewählt werden können, sowie ganze Zahlen (10) oder Dezimalzahlen (10.12).
Dann wird noch die Methode der Berechnung ausgewählt:
- Lösen, indem das Quadrat (Standard) vollendet wird.
- Lösen, indem die quadratische Formel verwendet wird.

Das Ergebnis
Wir haben wie in unserem Beispiel mit quadratischer Formel berechnet. Die zweite Möglichkeit ist die Berechnung der vollständigen Lösung nach Standard. Hier ist das Ergebnis wesentlich umfangreicher und länger.
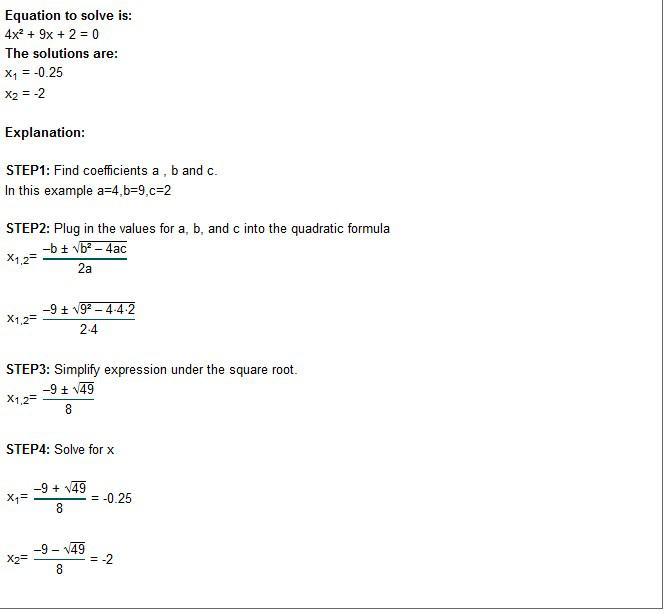
Bei der Berechnung der quadratischen Ergänzung wird nach einem bestimmten Schema vorgegangen:
1. die Koeffizient von x2 aus x2 und x ausklammern
2. quadratische Ergänzung
3. die negativen Term der quadratischen Ergänzung ausmultiplizieren
4. die binomische Formel auf die Klammer anwenden
Koeffizient = die Zahl, die als Faktor in einem Term mit Variablen steht. Beispiel: 2 und 5 beim Term 2×3+5x, also das was vor dem x steht.
Die binomischen Formeln
Wir kennen 3 binomische Formeln, die hier noch einmal zur Erinnerung inkl. ihrer Herleitung angeführt sind, denn es gilt bekanntermaßen in der Mathematik
Punktrechnung geht vor Strichrechnung
Klammern ausmultiplizieren
1. binomische Formel
( a + b )2 = a2 + 2ab + b2
Herleitung: ( a + b )2 = ( a + b ) · ( a + b ) = a2 + ab + ba + b2 = a2 + 2ab + b
2. binomische Formel
( a – b )2 = a2 – 2ab + b2
Herleitung: ( a – b )2 = ( a – b ) · ( a – b ) = a2 – ab -ba + b2 = a2 – 2ab + b2
3. binomische Formel
( a + b ) ( a – b ) = a2 – b2
Herleitung: (a + b) ( a – b ) = a2 -ab + ba -b2 = a2 – b2
Bei der Lösung, indem das Quadrat (Standard) vollendet wird, ist die Berechnung noch um einiges umfangreicher um Gegensatz zur Lösung nach quadratischer Formel.
Aufgrund der ziemlich umfangreichen Berechnungen mithilfe von verschiedenen Formeln ist unser Rechner eine wertvolle Hilfe.

