Winkelfunktion – alpha berechnen
Berechnen Sie die Winkelfunktion (alpha). Geben Sie hierzu folgende Basisdaten ein:
Länge der Ankathete
die Länge der Gegenkathete
die Länge der Hypothenuse.
Stell uns deine Frage. Wir antworten dir schnellstens...
Sie beschäftigen sich mit Geometrie oder Mathematik und wollen die Winkelfunktion alpha berechnen lassen? Mit dem Hilfreiche-Tools-Rechner können Sie diese einfach, kostenlos und schnell berechnen.
Die Winkelfunktion ? (alpha)
Jeder von uns kennt wohl noch den Lehrsatz von Pythagoras, wenn es im Schulunterricht um Geometrie oder Mathematik um die Berechnung von diversen Größen bei Dreiecken ging. In der Fachsprache nennt sich die Lehre von der Dreiecksberechnung mit Hilfe von Winkelfunktionen auch Trigonometrie und die Winkelfunktionen auch als trigonometrische Funktionen. Wesentlich bei diesen trigonometrischen Funktionen beziehungsweise der Winkelfunktion ? (alpha) ist, dass sich die Winkel und Seitenlängen eines Dreieckes, also sämtliche Größen von rechtwinkligen Dreiecken auch dann berechnen lassen, wenn nur eine Seite und ein angrenzender Winkel bekannt sind.
Aus der Schule sind eventuell auch noch Eselsbrücken wie „Geh Heim – Altes Haus – Gib Acht – Aufs Geld” oder „Gustav Hausers – Alte Hennen – Gackern Am – Abend Gerne, um uns die Berechnungsweise von Winkelfunktionen wie Sinus, Cosinus (Kosinus), Tangens und Cotangens (oder Kotangens) in deren korrekter Reihenfolge zu merken. Mit dem Hilfreiche-Tools-Rechner können Sie diese Winkelfunktionen sogar noch einfacher berechnen lassen.
Wie der Winkelfunktion alpha-Rechner funktioniert
Berechnen Sie hier die Winkelfunktion ? (alpha) sowohl für Sinus, Cosinus/Kosinus, Tangens und Cotangens/Kotangens beziehungsweise den jeweiligen gesuchten Winkel, ohne anschließende Umwege über die Umkehrfunktionen wie arcsin, arccos oder arctan am Taschenrechner.
Alles was Sie zur Berechnung des Winkels ? (alpha) benötigen, ist die Länge von zwei der drei einzugebenden Einheiten (Ankathete, Gegenkathete, Hypotenuse). Die Eingaben müssen hiebei in derselben Einheit, beispielsweise in Zentimetern, erfolgen.
Betätigen Sie anschließend die „Berechnen”-Taste, und als Ergebnis erscheint sofort die Größe des Winkels ? (alpha) im Textfeld.
Beispiel 1:
Berechnet werden soll die Sinus-Winkelfunktion, entsprechend der Formel „Gegenkathete durch Hypotenuse” (Eselsbrü >Ein Dreieck, das einen rechten Winkel (90 Grad) enthält, wird als rechtwinkliges Dreieck bezeichnet
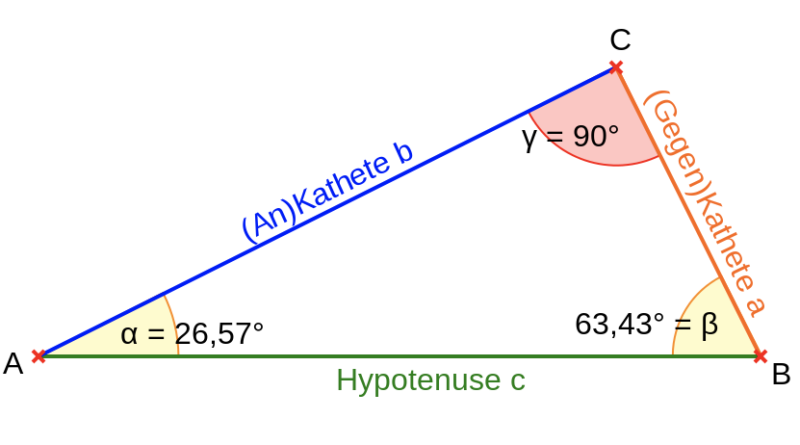
- Zur Kennzeichnung der Ecken eines Dreiecks werden Großbuchstaben (A, B, C) verwendet, die gegen den Uhrzeigersinn eingesetzt werden
- Zur Beschriftung der Seiten eines Dreiecks werden Kleinbuchstaben (a, b, c) verwendet, wobei die Seite a gegenüber dem Eckpunkt A liegt
- Zur Beschriftung der Winkel eines Dreiecks werden griechische Buchstaben (?, ?, ? – alpha, beta, gamma) verwendet, wobei sich der Winkel ? (alpha) beim Eckpunkt A befindet
- Die Winkelsumme in einem Dreieck beträgt stets 180 Grad
Ankathete, Gegenkathete und Hypotenuse
Die Seiten eines rechtwinkligen Dreiecks können nicht nur mit den Kleinbuchstaben a, b und c, sondern auch mit den Bezeichnungen Ankathete, Gegenkathete und Hypotenuse versehen werden. Die Seite, welche dem rechten Winkel gegenüberliegt, wird als Hypotenuse bezeichnet und ist in jedem Fall auch die längste Seite im rechtwinkligen Dreieck.
Als Kathete werden die beiden kürzeren Seiten eines rechtwinkligen Dreiecks bezeichnet, welche auch den rechten Winkel bilden.
Im Laufe der Zeit haben sich für diese Seiten die Begriffe Ankathete und Gegenkathete herausgebildet. Grundsätzlich gilt: Die dem Winkel anliegende Kathete nennt sich Ankathete. Die dem betreffenden Winkel gegenüberliegende Seite nennt sich Gegenkathete.
Es gibt sowohl eine Ankathete und Gegenkathete für den Winkel ? als auch für den Winkel ?, denn die Bezeichnung hängt davon ab, welcher dieser beiden spitzen Winkel im Mittelpunkt der Betrachtung steht. In rechtwinkligen Dreiecken ist also die Ankathete des Winkels ? (alpha) gleichzeitig die Gegenkathete des anderen spitzen Winkels ? (beta).
Wissenswertes zum Thema Winkelfunktionen
- Winkelfunktionen dienen dazu, das Verhältnis zweier Seiten in einem rechtwinkligen Dreieck zu definieren
- Wenn der Winkel ? (alpha) bekannt ist, lassen sich mithilfe einer beliebigen anderen bekannten Kanten- beziehungsweise Seitenlänge des Dreiecks alle anderen Seitenlängen berechnen
- Da die Winkelsumme im Dreieck stets 180 Grad beträgt und ein rechter Winkel 90 Grad hat, beträgt die Summe der beiden spitzen Winkel 90 Grad
- Daraus lässt sich die Berechnung folgern: der Winkel ? (beta) ist 90 abzüglich Winkel ? (alpha)
- Diese Grundsätze für Verhältnisse von Winkeln und Seiten gelten für jegliche Art von rechtwinkligem Dreieck, da die Verhältnisse aller Faktoren dieses Dreiecks stets den gleichen Wert haben
Berechnung der Winkelfunktionen in der Praxis
Die Kenntnis und die Berechnung von Winkelfunktionen oder trigonometrischen Funktionen ist nicht nur im Schulunterricht zu Grundsätzen der Geometrie wichtig. In der Praxis kommen Winkelfunktionen hauptsächlich im Vermessungswesen und in der Architektur vor. Diese Winkelfunktionen sind ebenso unerlässlich, wenn es um viele Anwendungen in der Physik und Technik geht. Auch in der mathematischen Analysis sind Winkelfunktionen unumgänglich. Es gibt eine enge mathematische Beziehung zwischen der Trigonometrie und der Exponentialfunktion, was beispielsweise besonders deutlich wird, wenn es um die Darstellung komplexer Zahlen oder die sogenannte Taylorreihe geht.
Sowohl in der Architektur als auch der Technik wird die Winkelfunktion sehr häufig zur Berechnung von Statik und baulichen Gegebenheiten verwendet. Denn viele auf den ersten Blick kompliziert aussehende geometrische Formen können sich in mehreren Stufen auf rechtwinklige Dreiecke zurückführen und daher leichter berechnen. Denn wie bereits erwähnt, es lassen sich Seitenlängen von rechtwinkligen Dreiecken berechnen, wenn nur eine Seite und ein angrenzender Winkel bekannt sind.
Quellen: wikipedia, mathebibel.de, frustfrei-lernen.de
Wichtig: Der Winkelfunktion-Alpha-Rechner und die im Artikel enthaltenden Informationen sind nur zu Ihrer Orientierung gedacht und erheben, trotz unserer gründlichen Recherche, keinen Anspruch auf Vollständigkeit und Richtigkeit. Wir beantworten gerne Fragen zum Winkelfunktion-Alpha-Rechner, übernehmen jedoch keinerlei Haftung, Verantwortung und Gewährleistung für die Ergebnisse.
Häufig gestellte Fragen
Was versteht man unter der Winkelfunktion (alpha)?
Was versteht man unter Gegenkathete, Ankathete und Hypotenuse?
Wie berechnet man die Winkelfunktion (alpha)?
Wozu benötigt man in der Praxis die Berechnung der Winkelfunktion?
Praxisbeispiel zur Berechnung der Winkelfunktion (alpha)
Häufig gestellte Fragen
Was versteht man unter der Winkelfunktion (alpha)?
Winkelfunkionen ganz allgemein sind in der Geometrie weit verbreitet. Sie werden genutzt, um die Zusammenhänge zwischen verschiedenen Achsen oder Kanten geometrischer Gebilde mathematisch zu beschreiben. Meist wird die Winkelfunkion a fälschlicherweise in Verbindung mit mit dem „Satz des Pythagoras“ genannt. Doch dieser beschreibt an sich nur die Seitenlängen eines rechtwinkligen Dreiecks – mit der Winkelfunkion a dagegen lassen sich aber auch rechtwinklige Dreiecke berechnen, wenn nur eine Seite und ein angrenzender Winkel bekannt ist!
Zum weiteren Verständnis der Winkelfunkion a wird vorausgesetzt, dass die zugehörigen Grundfunktionen Sinus, Cosinus und Tangens mit einem Taschenrechner berechnet werden können.
Was versteht man unter Gegenkathete, Ankathete und Hypotenuse?
Stellt man sich ein rechtwinkliges Dreieck vor, so ist die Seite, die dem rechten Winkel (also dem Winkel mit 90°) gegenüber liegt, immer die Hypotenuse. Sie ist automatisch auch die längste Seite in einem rechtwinkligen Dreieck.
Benennt man nun einen der anderen beiden Winkel mit dem griechischen Buchstaben a, so wird die direkt an diesem Winkel anliegende Seite als Ankathete bezeichnet (bitte nicht mit der Hypotenuse verwechseln!), die dem Winkel gegenüber liegende Seite heißt entsprechend Gegenkathete.
Wie berechnet man die Winkelfunktion (alpha)?
Unter Zuhilfenahme des als bekannt angenommenen Winkels a und einer beliebigen anderen Kantenlänge des Dreiecks lassen sich schrittweise alle anderen Seitenlängen bestimmen:
sin (a) = Gegenkathete / Hypotenuse
cos (a) = Ankathete / Hypotenuse
tan (a) = Gegenkathete / Ankathete
(Die Namen der drei Seiten stehen stellvertretend für die Längen der Seiten.)
Wichtig ist, dass die Angabe des Winkels a in allen gezeigten Formeln immer im Bogenmaß (rad) und nie im Gradmaß (°) erfolgt:
aBogenmaß = aGradmaß * 2* p / 360° (in radiant)
Wozu benötigt man in der Praxis die Berechnung der Winkelfunktion?
Die Berechnung mit Hilfe von Winkelfunkionen wird in der Technik wie auch in der Architektur sehr häufig verwendet. Viele kompliziert aussehende geometrische Formen lassen sich meist in mehreren Stufen auf rechtwinklige Dreiecke zurückführen.
Praxisbeispiel zur Berechnung der Winkelfunktion (alpha a)
Von einem Dreieck sind folgende Daten bekannt:
Seite a = 10 cm (Ankathete)
Anliegender Winkel a = 30° (alpha)
Anliegender Winkel c = 90° (gamma)
Zu berechnen sind alle anderen Seitenlängen und der verbleibende Winkel b.
Berechnung des Winkels b
Da die Summe aller Winkel in einem Dreieck immer 90° beträgt, ergibt sich:
b = 180° - a – c
Für die weitere Berechnung wird a zunächst ins Bogenmaß umgerechnet:
aBogenmaß = aGradmaß * 2* p / 360° (in radiant)
= 30° * 2* p / 360°
= 0,523 rad
Berechnung der Hypotenuse
Durch Umstellung der oben gezeigten Formel erhält man:
Hypotenuse = Ankathete / cos (a)
= 10 cm / cos (0,523)
= 11,54 cm
Berechnung der Gegenkathete
Durch Umstellung der oben gezeigten Formel erhält man:
Gegenkathete = tan (a) * Ankathete
= tan (0,523) * 10 cm
= 5,75 cm
Praxisbeispiel zur Berechnung der Winkelfunktion (alpha)
Von einem Dreieck sind folgende Daten bekannt:
Seite a = 10 cm (Ankathete)
Anliegender Winkel = 30° (alpha)
Anliegender Winkel = 90° (gamma)
Zu berechnen sind alle anderen Seitenlängen und der verbleibende Winkel b.